Sample Size Calculators

Statistical Power Information Confidence Interval Statistical Power Calculators
#CalculatorRelevant Tests
1Survey sample size.
Confidence interval sample size.		Proportion confidence interval.
Confidence interval.
2T sample size.
Z sample size.		One sample Z-test.
One sample T-test.
Two sample Z-test.
Two sample T-test (Pooled variance).
Two sample T-test (Welch's).
3Chi-Squared sample size.Chi-Squared test for goodness of fit.
4Regression sample size
ANOVA sample size.		Simple linear regression.
Multiple linear regression.
ANOVA.
5MANOVA sample size.MANOVA.
6F sample size.F test for variances.
7Proportion sample size.One sample proportion test.
Two sample proportion test.

A larger sample size generates more accurate results, but it may be more expensive.
You may calculate the sample size based on the required margin of error of the confidence interval or based on the required test power or using a rule of thumb.

Required Confidence Interval

The calculator determines the sample size to gain the required margin of error (MOE).
Confident Interval = Estimated value ± MOE .

A larger sample size reduces the margin of error.

Required Test Power

The calculator determines the sample size to gain the required test power and draw the power analysis chart.
A larger sample size increases the statistical test power.

Researchers usually use the power of 0.8 which mean the probability of type II error (β), failure to reject an incorrect H0.2, is 0.2. The commonly used significance level (α) is 0.05. β is usually four times bigger than α, since rejecting a correct null assumption consider to be more severe than failing to reject a correct invalid assumption.

Power Analysis Chart

The calculators create the following dynamic chart. When using the calculators, you may hover over any column any see the test power for each sample size.

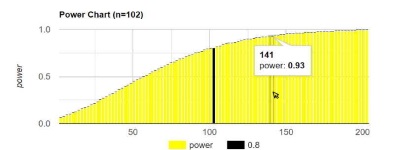
Z statistic

The chart shows the power per each sample size.
The black bar shows the sample size that achieves the required power. In this example 102 achieves the power of 0.8.
When you hover over the power chart in the calculator, you may see the sample size and the power it achieves. In this example a sample size of 141 achieves the power of 0.93.