Statistical power calculators
This webpage contains a free set of statistical test power calculators.
The power of a test is the probability of rejecting the null hypothesis, H0, when it is false.
The test power calculator computes the test power based on the sample size and effects size and generates an accurate power analysis chart.
A larger sample size increases the statistical power.
Power = 1- β.
β is the probability of a Type II error, which occurs when the null hypothesis fails to be rejected even though it is false.
Researchers usually choose a power of 0.8, meaning the Beta level (β), the maximum probability of Type II error, or failure to reject an incorrect H0, is 0.2.
The commonly used significance level (α), which represents the maximum probability of type I error, is 0.05.
In this case the Beta level (β) is four times larger than the significance level (α), as rejecting a true null hypothesis is considered more severe than failing to reject a false null hypothesis.
Power analysis chart
All the calculators generate the following chart based on the real values you entered and the calculations performed by the calculator.
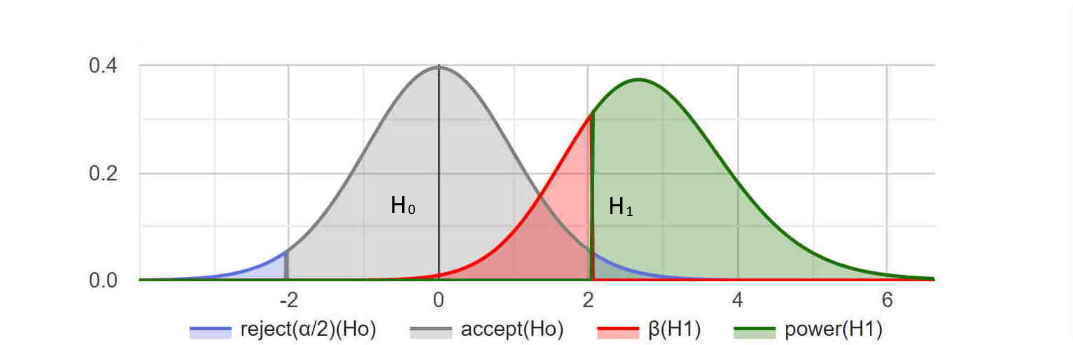
Region of Acceptance: Accept the null hypothesis (H0) if the test statistic falls within this region.
Region of Rejection: Reject the null hypothesis (H0) if the test statistic falls within this region.
Grey area: The probability of accepting H0 when H0 is true.
Significance level (α): The probability of Type I error, rejecting H0 when H0 is true.
Beta (β): The probability of Type II error, failing to reject H0 when H0 is false.
Test power: The probability of rejecting H0 when H0 is false.