ANOVA Calculator

One-Way ANOVA Calculator and Tukey HSD

 Enter raw data directly
 Enter raw data from excel

Enter sample data directly

Header: You may change groups' names to the real names.
Data: When entering data, press Enter or , (comma) after each value.
You may paste full column from excel.
The calculator ignores empty cells or non-numeric cells.

ANOVA

What is the ANOVA?

The ANOVA test checks if the difference between the averages of two or more groups is significant, using sample data.
ANOVA is usually used when there are at least three groups since for two groups, the two-tailed pooled variance t-test and the right-tailed ANOVA test have the same result.
The basic ANOVA test contains only one categorical value, one-way ANOVA. For example, if you compare the performence of three schools, the categorical variable is school, and the possible values of the categorical variable are School-A, School-B, School-C. There are more complex ANOVA tests that contain two categorical variables ( Two-way ANOVA calculator ), or more. When performing a one-way ANOVA test, we try to determine if the difference between the averages reflects a real difference between the groups, or is due to the random noise inside each group.
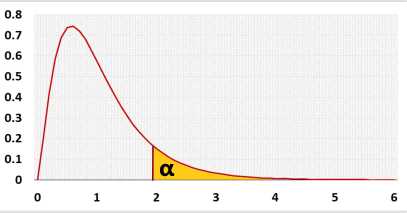
The F statistic represents the ratio of the variance between the groups and the variance inside the groups. Unlike many other statistic tests, the smaller the F statistic the more likely the averages are equal.

Example: Compare four fertilizers used in four fields
H0: The average weight of crops per square meter is equal in all fields.
H1: At least one field yields a different average per square meter.

Right-tailed, for ANOVA test you can use only the right tail. Why?
Hypotheses
H0: μ1 = ... = μk
H1: not(μ1 = ... = μk)
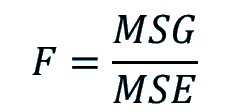
ANOVA formula
anova formula
F distribution
F distribution right tailed

Assumptions

  • Independent samples
  • Normal distribution of the analyzed population
  • Equal standard deviation, σ1=σ2=...=σk
    The assumption is more important when the groups' sizes not similar

Required Sample Data

  • Sample data from all compared groups

Parameters

  • k - Number of groups.
  • ni - Sample side of group i
  • n - Overall sample side, includes all the groups (Σni, i=1 to k)
  • x̄i - Average of group i.
  • x̄ - Overall average (Σxi,j / n, i=1 to k, j=1 to ni)
  • Si - Standard deviation of group i

Results calculations

SourceDegrees of FreedomSum of SquaresMean SquareF statisticp-value
Groups
(between groups)		k - 1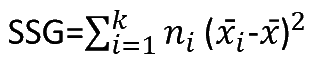averageMSG = SSG / (k - 1)F = MSG / MSEP(x > F)
Error
(within groups)		n - k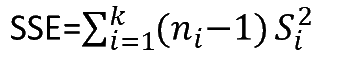averageMSE = SSE / (n - k)
Totaln - 1SS(total) = SSG + SSESample Variance = SS(total) / (n - 1)