Levene's test calculator

Levene's test

The Levene's test checks if the difference between the variability of two or more groups is significant.
The Levene's test doesn't compare the variances, but compare the Mean Absolute Deviations (MAD), which is another way to check the data variability, on the other hand if the MADs are not the same, very likely that the variances are not the same.

The Levene's test perform an ANOVA test over the absolute deviations from each group's center.
The group center may be the mean or the median. When using the mean as group center the test is called the Levene's test, when using the medain as group center the test is called the brown forsythe test.

When performing ANOVA test, we try to determine if the difference between the MADs reflects a real difference between the groups, or is due to the random noise inside each group. The F statistic represents the ratio of the variance between the groups and the variance inside the groups. Unlike many other statistic tests, the smaller the F statistic the more likely the averages are equal.

Right-tailed F test, for ANOVA test you can use only the right tail. Why?

Hypotheses

H₀: σ₁ = .. = σ_k

H₁: not(σ₁ = .. = σ_k)

Test statistic

F =	MSG
	MSE

F distribution

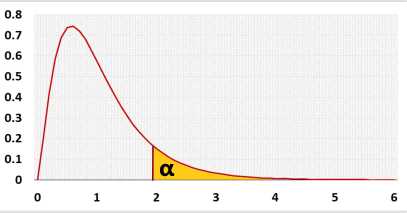
Assumptions

• Independent observations (no repeated measure)
• The dependent variable is continuous (ratio or interval)
• The independent variable is categorical, contains the groups' name.
• The residuals distribution is normal, or sample size of 30 or more and reasoabily symetrical

Required Sample Data

Sample data from all compared groups.

ANOVA table formulas

Parameters

k - number of groups.
n_i - sample side of group i.
n - overall sample side, includes all the groups (Σn_i, i=1 to k).
x̄_i - average of absolute differences from group's average, in group i.
x̄ - overall average (Σx_i,j / n, i=1 to k, j=1 to n_i).
S_i - standard deviation of group i.

For the levene's, each value is the difference from the group's center.

Source	Degrees of Freedom	Sum of Squares	Mean Square	F statistic	p-value
Groups (between groups)	k - 1		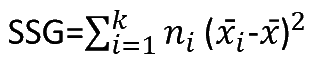MSG = SSG / (k - 1)	F = MSG / MSE	P(x > F)
Error (within groups)	n - k		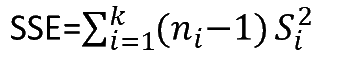MSE = SSE / (n - k)
Total	n - 1	SS(total) = SSG + SSE	Sample Variance = SS(total) / (n - 1)