T-test (Student's t-test)

The t-test is not one test, but a group of tests that constitutes all statistical tests distribute as t-distribution (Student’s t-distribution).
We use the t-test(s) to compare the sample average (Mean) to the known mean or to compare the averages of two groups when we don’t know the standard deviation, and use the sample standard deviation.
When we know the standard deviation value, for example from another research, we use the z-test, but usually, we have only the sample standard deviation.

When the sample is greater than 30 you should still use the t-distribution, although using the normal distribution instead will support similar results. Student's T distribution is an artificial distribution used for a normally distributed population when we don't know the population's standard deviation. The data distribute

T distribution looks similar to the normal distribution but lower in the middle and with thicker tails. This makes it more realistic than Normal distribution since for small sample sizes, the average and standard deviation estimations are less accurate

The shape depends on the degrees of freedom which is usually the number of independent observations minus one (n-1). The higher the degree of freedom the more it resembles the normal distribution.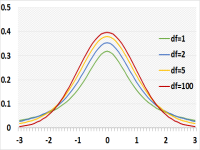

t-distributions for several degrees of freedoms

One-sample t-test (go to the calculator)

What is the one-sample t-test?

The one-sample t-test checks if the known mean is statistically correct, based on a sample average and sample standard deviation.
The null hypothesis assumes that the known mean is correct. The statistical decision will be based on the difference between the known mean and the sample average.

Example: A farmer calculated last year the average weight of apples in his orchard (μ0) is 17 kg, based on a big sample.
This year he checks a small sample of apples and the sample average x is 18 kg.
Did the average weight of apples change over the past year?

What are the one-sample t-test assumptions?

Independent samples
The population has a normal distribution.
The standard deviation of the population is unknown, the sample size is small or both
The population mean is known

What data do you need to calculate the one-sample t-test?

Calculated based on a random sample from the entire population

x̄ - Sample average
S - Sample standard deviation
n - Sample size

What is the one-sample t-test formula?

t =	x̄ - μ₀
	S / √n

How to perform a one-sample t-test in R?

x1 <- c(160.2, 151.2, 165.8, 189.3, 173.3)
t.test(x1, x2 = NULL, alternative = "two.sided", paired = FALSE, mu = 190, conf.level = 0.95)

For one sample x2 is NULL.
mu - the expected difference, in this example mu=190.

Two-sample t-test - equal variances (pooled-variance) (Go to the calculator)

What is the two-sample equal variances t-test?

The Two-sample t-test - equal variances also called independent t-test compares the population means (averages) of two independent groups. It may check if the means are equal, or if the known difference between the mean is correct.
The test assumes that the standard deviations are identical for both groups.

The null hypothesis (H₀) assumes that the known difference between the groups is correct. When the known difference is zero, the null hypothesis assumes the means of the groups are identical.

What are the two-sample t-test assumptions?

Independent samples
Independent groups
Both groups have normal distributions
Unknown standard deviation
Both groups have equal standard deviations.
If this assumption is incorrect. The test will not supply good results.
The difference (d) between the means of both groups' means is known.

What data do you need to calculate the two-sample t-test?

A few statistical inputs are calculated based on a random sample from the entire population:

x̄_i - Sample average of group i
S_i - Sample standard deviation of group i
n_i - Sample size of group i

What is the two-sample t-test formula?

t =	x̄₁ - x̄₂ - d
	S / √(1/n₁ + 1/n₂)

S²=	(n₁ - 1)S₁² + (n₂ - 1)S₂²
	n₁ + n₂ - 2

df = n₁ + n₂ - 2 (degrees of freedom)

How to perform a two-sample t-test in R?

x1 <- c(160.2,151.2,165.8,189.3,173.3)
x2 <- c(156.1,160.1,163.3,182.4,172.4)
t.test(x1, x2, alternative = "two.sided", paired = FALSE, var.equal = TRUE, conf.level = 0.95)

Two-sample t-test with unequal variances (Welch's t-test) (Go to the calculator)

What is Welch's t-test?

The two-sample t-test with unequal variances also called Welch's t-test compares the population means (averages) of two independent groups. It may check if the means are equal, or if the known difference between the mean is correct.
The test assumes that the standard deviations are not the identical for both groups.

The null hypothesis (H₀) assumes that the known difference between the groups is correct. When the known difference is zero, the null hypothesis assumes the means of the groups are identical. The assumptions and required sample data of the Welch’s T-test are similar to the Pooled-Variance T-test with one exception - this time we assume that the standard deviations of the groups are not the same.

What are Welch's t-test assumptions?

Independent samples
Independent groups
Both groups have normal distributions
Unknown standard deviation, a small amount of data, or both
Unequal variances, both groups don't have the same standard deviation.
If this assumption is incorrect. The test will still supply reasonable results
The difference (d) between the means of the groups is known.

What data do you need to calculate Welch's t-test?

A few statistical inputs are calculated based on a random sample from the entire population:

x̄_i - Sample average of group i
S_i - Sample standard deviation of group1 and group i
n_i - Sample size of group1 and group i

What is Welch's t-test formula?

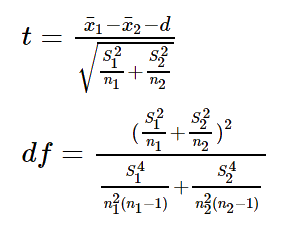
How to perform the Welch's t-test in R?

x1 <- c(160.2,151.2,165.8,189.3,173.3)
x2 <- c(156.1,160.1,163.3,182.4,172.4)
t.test(x1, x2, alternative = "two.sided", paired = FALSE, var.equal = FALSE, conf.level = 0.95)

How do you know if the standard deviation of the groups is the same?

If you have preliminary knowledge, it is an easy decision, but what happened if you don’t?

Using Welch’s T-test (unequal variances) with equal variance across samples will support reasonable results with relatively minor differences from the correct pooled-variance t-test (equal variances)
When using Pooled-Variance T-test (equal variances) with unequal variances across samples it will not support good results (unless using equal sample sizes)

The common practice was to run a test to compare the standard deviation, of the groups and then decide which t-test to run.

This method is not so recommended, as in the case of a type-2 error for the first step (failing to reject the null hypothesis) we assume that the standard deviations are equal while actually, it is not. In this case, we will run the pool-variance t-test instead of the unequal variances.

Conclusion

If you don’t know that the standard deviations are equal you should run Welch’s t-test (unequal variances)

Example Table: Error when using incorrect test pooled-variance t-test via Welch’s t-test

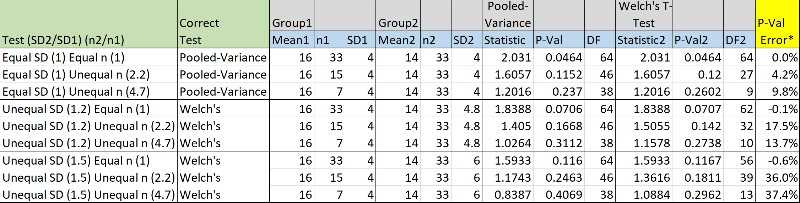
compare pool variance t-tests and Welch's tt-test

* P-Val Error = 1 - (Correct P-Val / Incorrect P-Val)

Paired T-Test (Go to the calculator)

What is the paired t-test?

The paired t-test compares the average of two dependent groups. The test compares the results of the same items in two different conditions.
For example the same subject before treatment and after treatment. ie: to test a new cholesterol pill, an experiment is performed and results are collected before they took the pill and several days after. Unlike a regular T-test where there are two groups of people – one who took the pill and one who didn’t, this test constitutes the same group of people both before and after taking the pill.
The null hypothesis assumes that the expected difference between the groups is correct.
Usually, the expected difference is zero, in this case the null hypothesis assumes the means of the groups are identical

What is the advantage of the paired t-test?

Since we use the same subjects in the two groups it reduces the random noise between the groups, and this increase the test power. On the other hand, the sample size is the number of pairs which is half of the number of observations, this reduces the test power.
But overall the paired t-test is considered more powerful than the two-sample t-test.
It is usually easier to measure twice, half of the subjects.

What are the paired t-test assumptions?

Independent paired samples
Dependent groups - dependency inside each pair
The population's distribution approaches the normal distribution
The difference (d) between the mean of the groups is known
Expected difference between any paired samples

What data do you need to calculate the paired t-test?

X_d = calculate the difference for each pair
x̄_d – the average of the differences of each pair, d_i = X_2,i - X_1,i
S_d – the standard deviation of the differences
M₀ – expected difference between the two groups
n – number of pairs (not number of subjects)

What is the paired t-test formula?

t =	x̄_d - μ₀
	S_d / √n

df = n - 1, the degrees of freedom equals the number of pairs minus one (or number of observation divided by 2 minus 1)

How to perform paired t-test in R?

x1 <- c(160.2,151.2,165.8,189.3,173.3)
x2 <- c(156.1,160.1,163.3,182.4,172.4)
t.test(x1, x2, alternative = "two.sided", paired = TRUE, mu = 0, conf.level = 0.95)

mu - the expected difference, usually zero.

How do you check the normality assumption on the t-test?

You may run the Shapiro-Wilk test on the data, check the p-value, the Q-Q plot and the histogram.

What if the sample size is very small?

When the sample size is very small, as a rule of thumb less than 15, the SW test doesn't have enough data to decide if the distribution is normal.
If you have prior data from other researches that the distribution is normal, you may use the t-test, otherwise you should consider a non-parametric test.

What if the sample size is large?

When the sample size is large, as a rule of thumb 30 or more, the average's distribution may be similar to the normal distribution (CLT).
In this case event if the SW test rejected the normality assumption, if the histogram is reasonably symmetrical you should use the t-test.

T-test calculators

References:

The following reference was titled for psychologists, albeit it is relevant to any category