Multiple Linear Regression Calculator

Multiple regression calculator with unlimited predictors.

Video Information Simple linear regression Regression sample size
Constant is zero (Force zero Y-intercept, b0=0)
Power regression - Ln transformation (natural log) over all the variables: Y=exp(b0)⋅X1b1⋅⋅Xpbp .
  Enter raw data directly
  Enter raw data from excel

Header: You may change the groups' names to their real names.
Data: When entering data, press Enter or Comma , or Space after each value.
* All variables will be included in the automatic iterations mode.
** Normality colors based on α=0.05

Reporting results in APA style


Multiple linear regression calculator

The calculator uses variables transformations, calculates the Linear equation, R, p-value, outliers and the adjusted Fisher-Pearson coefficient of skewness.
After checking the residuals' normality, multicollinearity, homoscedasticity and priori power, the program interprets the results.
Then, it draws a histogram, a residuals QQ-plot, a correlation matrix, a residuals x-plot and a distribution chart.
You may transform the variables, exclude any predictor or run backward stepwise selection automatically based on the predictor's p-value.

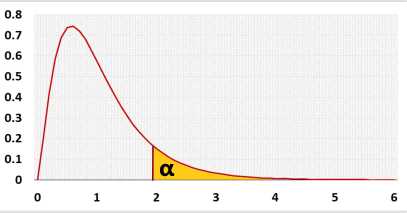
Right-tailed F test. Checks if the entire regression model is statistically significant. Why?

Multiple linear regression formula

Y = b0 + b1X1 + b2X2 + b3X3+...+ bpXp + ε
It is easier to use the matrix form for multiple linear regression calculations:
Y = XB + Ε
Ŷ = XB
B = (X'X)-1X'Y
[1 X11 X12 ... X1p][Y1]ε1]
[1 X21 X22 ... X2p][Y2][ε2]
X = [1 X31 X32 ... X3p]    Y = [Y3]   Ε = [ε3]
[1 X41 X42 ... X4p][Y4][ε4]
[1 Xn1 Xn2 ... Xnp][Yn][εn]
[B0]
[B1]
B = [B2]
[... ]
[Bp]
Y - dependent variable vector.
Ŷ - predicted Y vector.
Ε - residuals vector, Ε = Y - Ŷ.
p - number of predictors.
n - sample size.
Hypotheses
H0: Y = b0
H1: Y=b0+b1X1+...+bpXp
Test statistic
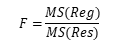
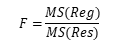
F statistic
F distribution
F distribution right-tailed