ROC Calculator

How to use the ROC curve calculator

ROC curve calculator with optional Excel input, offering customization options such as fonts and colors. It allows users to plot and compare multiple Receiver Operating Characteristic (ROC) curves simultaneously on a single graph.

Process

1. Enter the data:
2. Press the 'Calculate' button to get the results.
3. Press the camera icon that appears when you hover over the chart to save the chart as an image.

How to enter data?

• Enter data in columns
• • Enter the curve name, the default is 'Curve1'.
  • Score - the score value used to predict the actual outcome.
  • Actual outcome - the binary result that the model is trying to predict; it can be either 0 or 1.
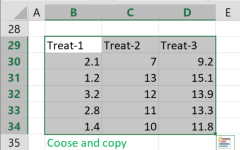
  • Enter the raw data separated by 'comma', 'space', or 'enter'. (*in you may copy only the data from excel).
• Enter data from Excel
  
  1. Copy Paste
     
     • a. copy the raw data with the header from Excel or Google sheets, or any tool that separates data with tab and line feed. copy the entire block, include the header .
     • Paste the data in the input field.
  2. Import data from an Excel or CSV file.
     When you select an Excel file, the calculator will automatically load the first sheet and display it in the input field. You can choose either an Excel file (.xlsx or .xls) or a CSV file (.csv).
     To upload your file, use one of the following methods:
     1. Browse and select – Click the 'Browse' button and choose the file from your computer.
     2. Drag and drop – Drag your file and drop it into the 'Drop your .xlsx, .xls, or .csv file here!' area.
     Once the file is uploaded, the descriptive statistics calculator will display the data from the first sheet in the input field.
     Now, the 'Select sheet' dropdown will be populated with the names of your sheets, and you can choose any sheet.

Customization Options

The options already contains default values.

1. Title - the title of the ROC curve.
2. Y-Axis Label - the default is 'True Positive Rate', you may change to other labels like 'TPR' or 'Sensitivity'
3. X-Axis Label - the default is 'False Positive Rate', you may change to other labels like 'FPR' or '1 - Specificity'
4. Rounding - how to round the results?
   When a resulting value is larger than one, the tool rounds it, but when a resulting value is less than one the tool displays the significant figures.
5. Legend - the location of the legend, vertical or horizontal
6. Fonts - fonts' type, size, and color
7. Curve line - show line, marker, or both. Solid or dashed line. Line width.
8. Diagonal line - Solid or dashed line. Line width. Line color.
9. AUC - font size, font color
10. AUC line spacing - When having more than one curve, it is the amount of vertical space between lines of text (AUC or Max Cutoff)
11. AUC X - the horizontal location of the AUC or Max Cutoff.
12. AUC Y - the vertical location of the AUC or Max Cutoff.
13. AUC X Alignment: - the alignment of the AUC or Max Cutoff.
14. Tick interval - the distance or spacing between tick marks on the X-axis and Y-axis.
15. Enter data directly - delimiters:
    When you enter the data manually the default is pressing Enter after any value, but you may use other delimiters.

What is ROC curve?

In a binary classifier model, the Receiver Operating Characteristic (ROC) curve plots the True Positive Rate (TPR) on the y-axis against the False Positive Rate (FPR) on the x-axis. This is done across different thresholds.

What is AUC?

The Area Under the Curve (AUC) is the area under the ROC curve. The AUC reflects how well the model performs compared to a random decision.

• AUC > 0.5 represents a model that is better than a random decision.
• AUC = 0.5 represents a poor model that is no better than a random decision.
• AUC < 0.5 represents a model that is worse than a random decision. It indicates that the direction of the decision is incorrect, and we should reverse the decision. In this case, the new AUC will be greater than 0.5 (New AUC = 1 - AUC).

For example, if the model states that a person is sick when the test result is greater than 244, we should change it to indicate that the person is sick when the test result is less than 244.

Glossary

2. Test - classification model
3. Positive -
4. True Positive (TP) - the test predicted true, and the result is true
5. False Positive (FP) - the test predicted true, and the result is false
6. True Negative (TN) - the test predicted false, and the result is false
7. False Negative (FN) - the test predicted false, and the result is true
8. True Positive Rate (TPR), also called Sensitivity - the proportion of positive cases that the test identify from the total positive cases.
   $TPR = \frac{TP}{TP+TN}$
9. False Negative Rate (FPR), also equals (1 - specificity) - this is the - the proportion of false negative cases that the test identify from the total negative cases.
   $FPR = \frac{FP}{FP+TN}$
10. Specificity - this is the True Negative Rate (TNR) - the proportion of negative cases that the test identify from the total negative cases.
    $TNR = \frac{TN}{FP+TN}$

AUC levels

• An AUC of 0.5 suggests no discrimination, meaning the model does no better than random chance.
• 0.5 - 0.6: is considered very poor.
• 0.6 - 0.7: is considered poor.
• 0.7 - 0.8: is considered acceptable.
• 0.8 - 0.9: is considered excellent.
• Greater than 0.9: is considered outstanding.