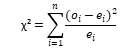Kaplan Meier Survival Analysis

Information

The Kaplan–Meier method is a non parametric method used for the survival analysis. The survival probability calculator generates the Kaplan-Meier curve with confidence interval and calculates the Log-Rank test for more than of two groups.
Event of interest (D_t): Maintenance failure, recovery, disease occurrence, death, etc.
Censored event (C_t): the event of interest didn't happen since the subject left the experiment before the ending time, or due to the termination of the experiment.
n_t: number of participants that didn't have an event yet (event of interest or censored event).
Proportion surviving interval (P_t): the proportion of survival participants between period t-1 and period t.
Survival rate (S_t / Cumulative Survival/ Survival function): the proportion of survival participants from period 0 to period t.
Sum = ΣD_t/n_t(n_t - D_t)
S.E_t: the standard deviation of the survival rate. S.E = S_t√(Sum)
Lower_t: Lower bound of S_t confidence interval .
Upper_t: Upper bound of S_t confidence interval.

Chart type

Line –Survival rate (St) per time.
Confidence interval – added the Confidence interval areas to the line, with confidence level of (1 - α).
S.E area – present S_t ± 1*S.E, the S.E is the area below and above the line.
S.E error bars – present S_t ± 1*S.E, the S.E is presented as error bar.

Log rank test calculator

Target: test the null assumption that the "time to event" distribution is identical for all the groups.
The test uses the chi-square distribution.

The log-rank test model assumes the events per subject distributes evenly between the groups. The expected number of events is calculated per each time value.
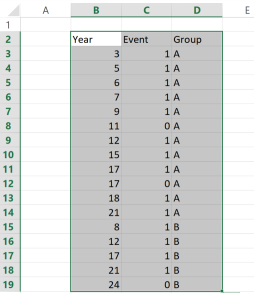
Example with two groups A and B.
Expected value = n_A(d_A + d_B)/(n_A + n_B)

The page was created per Anna P request.