Markov Chain Calculator
Calculates the nth step probability vector and the steady-state vector.
Transition matrix
Transition matrix - P, and the initial state vector.
Markov chain
Markov chain calculator and steady state vector calculator. Calculates the nth step probability vector, the steady-state vector, the absorbing states, and the calculation steps.
What is a Markov chain?
The Markov chain is a mathematical system used to model random processes by which the next state of a system depends only on its current state, not on its history.
This stochastic model uses discrete time steps. The Markov chain is a stochastic model that describes how the system moves between different states along discrete time steps.
There are several states, and you know the probability to move from any state to any state. If you can't move from one state to another state then the probability is zero.
What are discrete-time steps?
The change in the system is being done only in steps, between the steps the system remains in the same state.
When the step is triggered the system may move to another state or stay in the same state.
The time between the steps is not necessarily constant, for example in a board game each time player makes a move is a step.
What are the Markov chain assumptions?
- The Markov property - the history doesn't matter, the probability to move to each state depends only on the last state.
- The time stationarity property - the probability distribution doesn't depend on the step (n).
What is an absorbing state?
The absorbing state is a state that once entered, it is impossible to leave the state. In the transition matrix, the row that starts with this step
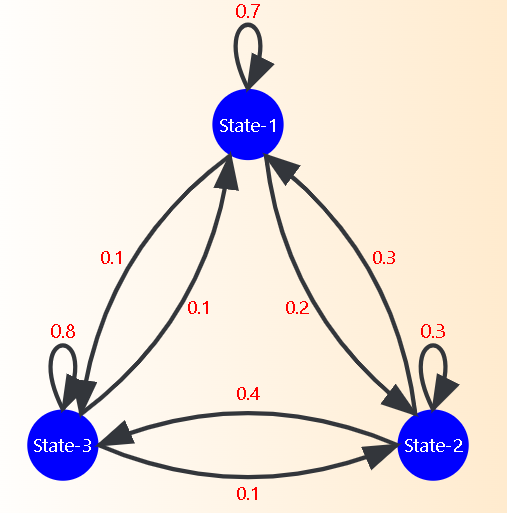
Example of Markov chain diagram
The following is an example of a three-state Markov chain. The one-step transition probabilities are as follows:
- The probability of moving from state A to state B is 0.6, while the probability of remaining in state A is 0.4.
- The probability of moving from state B to state C is 0.8, while the probability of remaining in state B is 0.2.
- The probability of moving from state C to state A is 0.7, while the probability of remaining in state C is 0.3.
All other transition probabilities, such as moving from state A to state C, are zero.
Markov chain formula
The following formula is in a matrix form, S0 is a vector, and P is a matrix.
P - transition matrix, contains the probabilities to move from state i to state j in one step (pi,j) for every combination i, j.
n - step number.
Sn - the nth step probability vector.
Example:
S0 = [p1, p2, p3]
| [p1,1, p1,2, p1,3] | |
| P= | [p2,1, p2,2, p2,3] |
| [p3,1, p3,2, p3,3] |
Enter data into the Markov chain calculator
- Enter the number of steps (n) - the result will be the probability vector after n steps.
- Press "Insert state" or "Delete state" to increase or decrease the number of states.
- Enter the initial state - what state do you start with? it may be also a probability combination of states. If you know the state, you should enter one (1) for the state to start with, and zero (0) for all other states.
- Enter the Transition matrix - (P) - contains the probability to move from state-i to state-j, for any combination of i and j.
For a combination of states, enter a probability vector that is divided between several states, for example [0.2,0.8,0,0]
In this example, you may start only on state-1 or state-2, and the probability to start with state-1 is 0.2, and the probability to start with state-2 is 0.8.
The initial state vector is located under the transition matrix.
What is the probability vector?
The probability vector shows the probability to be in each state. The sum of all the elements in the probability vector is one. The nth step probability vector (Sn) is the probability vector after n steps, when starting in the initial state. (S0)
What is the steady-state vector?
Usually, the probability vector after one step will not be the same as the probability vector after two steps.
But many times after several steps, the probability vector after n steps equals to the probability vector after n-1 steps.
To get the vector you need to solve the following equation, matrix form.
You need to find the eigenvector with eigenvalue equals 1, and then divide every element by the total, as the sum of probabilities must be 1.
Another method is to find the Pn matrix that meets the following equation, The vector will be any row in the Pn matrix.
When all the rows in the Pn matrix are identical, the initial state does not influence the result. It does not matter what state you started with, and there is only one vector.
When all rows in the Pn matrix are not identical, the initial state influences the result. In this case, there is more than one vector, and the vector depends on the state you started with.
When there is more than one vector and the initial state is not constant, the vector is the combination of the vectors of the relevant states:
Steady-state vector example
Transition matrix| P= | [0.7, 0.3] |
| [0.2, 0.8] |
[1, 0]
Steps
| Step | State-1 | State-2 |
|---|---|---|
| S0 | 1 | 0 |
| S1 | 0.7 | 0.3 |
| S2 | 0.55 | 0.45 |
| ... | ... | ... |
| S13 | 0.4001 | 0.5999 |
| S14 | 0.4 | 0.6 |
| S15 | 0.4 | 0.6 |
You may see that from step 14 the probability vector does not change: [0.4, 0.6].
S15 = S14.
More precisely, if we round to 10 decimal places, we can see it that the two vectors are not equal:
S14 = [ 0.4000366211, 0.5999633789].
S15 = [ 0.4000183105, 0.5999816895].
But when n -> ∞, Sn ->[0.4, 0.6].