One Sample Z-Test Calculator

Use the z-test when you know the population standard deviation

Video One Sample T-test Two Sample Z Test
or or enter summarized data (x̄, n, σ, S) below

Enter sample data

Header: You may change groups' name to the real names.
Data: When entering data, press comma , , Space or Enter after each value.

The tool ignores empty cells or non-numeric cells.

Enter sample data

You may copy data from Excel, Google sheets or any tool that separate data with Tab and Line Feed.
Copy the data, one block of 2 consecutive columns includes the header, and paste below.

Copy the data,

It is okay to leave empty cells, empty cells or non numeric cells won't be counted

1 - Not mandatory, uses to validate σ


The difference between the expected SD and the sample SD

When entering raw data, the tool will run the Shapiro-Wilk normality test and calculate outliers, as part of the test calculation.
validation message

Z test online

Target: To check if the assumed μ0 is statistically correct, based on a sample average.
You know the standard deviation from previous researches.

Example1: A farmer calculated last year the average of the apples' weight in his apple orchard μ0 equals 17 kg, based on the entire population.
The current year he checked a small sample of apples and the sample average x equals 18 kg
Has the average of the apples' weight changed this year?
The farmer know the standard deviation of the apple's weight from previous researches.

Hypotheses
H0: μ ≥ = ≤ μ0
H1: μ < ≠ > μ0
Test statistic
Z=x̄-μ₀σ/n
Normal distribution
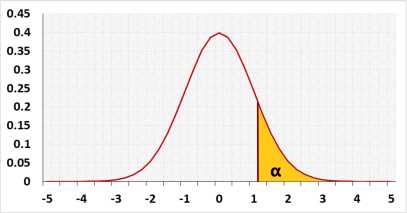
z distribution left tailed z distribution two tailed z distribution right tailed

Assumptions

Normal DistributionNormal distribution
standard deviationThe standard deviations of the population is known
meanPopulation expected mean is known

Required Sample Data

averageSample average
sample sizeSample size

R Code

The following R code should produce the same results:

Currently, there is no direct R function for the one-sample z test.



Examples
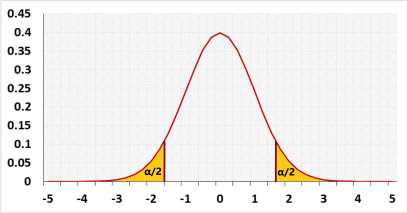
1. Two-tailed test
A farmer calculated last year the average of the apples' weight in his apple orchard μ0 equals 17kg, based on a big sample.
The current year the sample average x̄ equals 16kg.
Was the average of the apple's weight in the entire orchard changed this year? or is it just a random difference?

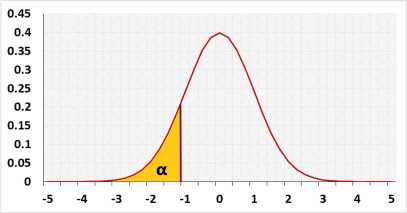
2. Left-tailed test.
In the same example as above, the farmer only cares to know if the entire average is lesser this year.