Logistic Regression Calculator

tails: using to check if the regression formula and parameters are statistically significant.
logistic Regression tutorial

Hypotheses

H0: ln(odds) = b0
H1: ln(odds) = b0+b1X1+...+bpXp

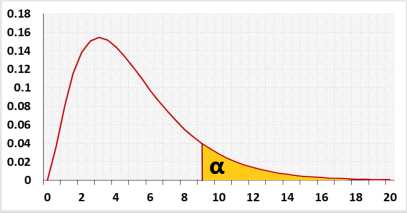
Test statistic

χ2 = 2(LL1-LL0)

χ2 distribution

F distribution right tailed

Test calculation

Statistic Data

Outliers:
Data Name: Every time you run the calculation, it will save your current data in the local storage.
α:Significant level (0-1), maximum chance allowed rejecting H0 while H0 is correct (Type1 Error)
Maximum iterations:Usually you shoudn't change this number
Iterations Delta:Usually you shoudn't change this number
Digits:When choosing 2 digits, 0.00001234 will be rounded to 0.000012

The dependent data (Y) can take multiple columns or be condensed into one.
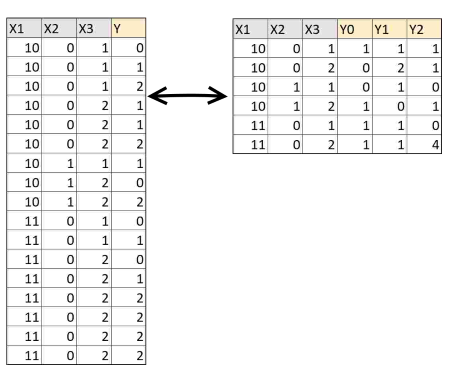
Click the following example, it contains the same data arange as one Y column or as several Y columns
example from excel

Enter raw data directly
Enter raw data from excel

Enter sample data directly

Header: You may change groups' name to the real names.
Data: When entering data, press Enter after each value.

Enter sample data from excel

Number of y columns: (When the value is 0, the tool will count automatically headers with "Y")

You may copy data from Excel, Google sheets or any tool that separate data with Tab and Line Feed.
Copy the data, one block of consecutive columns includes the header, and paste below.
Y must be the right columns. . click to see an example: example from excel



After the calculation, the tool will copy the data to the columns view for a better flexibility

The tool uses Newton's Method. Different methods may have slightly different results, the greater the log-likelihood the better the result.

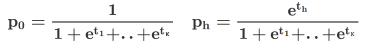
logistic probability formula

validation message

Newton's Method


Correlation matrix
tresults2