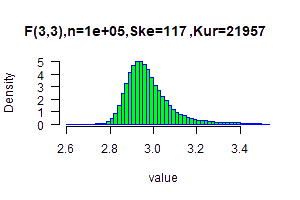Central Limit Theorem

What is the central limit theorem?
The average of large number of non-normal identical independent random variables usually distributes similar to the normal distribution.
As a result the sum or the proportion of large enough sample may distributes similar to the normal distribution.

Why is this important?
Many tests like t-test, ANOVA, F test for variances assumes a normal population.
It is easy to do calculations using the normal distribution, like confidence interval calculation, or any other probability calculation.

Example
You want to know the true mean of unknown distribution, what is the average of the entire population, not only the sample?.

1. Sample 100 random values.
2. Calculate the sample average: x, and the sample standard deviation S.
   The average of the sample is a random variable by itself, if you take 10 samples of 100 values, you will get a different average per each sample
3. If the CLT works you can assume that AVG distribution is similar to the normal distribution: $$N(\bar{x},\frac{S}{\sqrt{n}})$$ The confidence interval of the true mean is: $$\bar{x}\pm Z_{1-\frac{\alpha}{2}}\frac{S}{\sqrt{n}}$$

Limitations

Following the limitations for the classical CLT, there are different versions for the CLT that deal with part of the limitations.

• Independent variables
• Finite variance
• identical distributions

What sample size is large enough ?
In some cases a sample size of 30 observations is sufficient to assume the average distribute normally, for example for the t-test with reasonably symmetric data it is usually enough.
But as you may see in the below F(6,6) example, for highly skewed data, with undefined skewness level, only with 5000 observations the average distribute similar to normally. And But as you may see in the below F(3,3) example, for highly skewed data, with undefined skewness level, even the average of 100,000 kas skewed distribution.

Examples

Method

We used R statistical programming language to create a simulation of several distributions.

n - sample size
SAMPLE[n] - vector, with n values.
AVERAGES[repeats] - vector with repeats = 100,000 values. We chose 100,000 for a smooth histogram, 10,000 would also do a similar job.

Following process, for each sample size n:

1. Repeat 100,000 time the following process:

• Generate SAMPLE vector with n values of F(6,6).
• Insert average(SAMPLE) into AVERAGES vector.

2. Create histogram for AVERAGES vector.
3. Calculate the measurements of the AVERAGES vector.

• Skewness - skewness(avg1,method = c("moment"))
• Kurtosis - kurtosis(avg1,method = c("sample_excess"))
• Shapiro Wilk p-value - since the shapiro.test is limited to 5,000, we divides the repeats to blocks of 5,000 and calculate the average of the p-values.

Successful examples

In the following examples you may see that when the sample size is large enough the distribution is similar to the normal distribution.

F distribution

The F distribution is similar to the bell shape with different levels of skewness and kurtosis. $$F\ Skewness=\frac{(2df_1+df_2-2)\sqrt{8(df_2-4)}}{(df_2-6)\sqrt{df_1(df_1+df_2-2)}},\ df_2>6$$

Undefined skewed data: F(6,6) distribution

When DF₂≤6 the skewness of the original distribution is not defined.
Following a simulation results of F distribution with df₁=6 and df₂=6.
The calculated skewness( F(6,6) ) is undefined, and the simulation skewness is xxx.
The calculated excess kurtosis( F(6,6) ) is undefined, and the simulation kurtosis is xxx..
Only with extra large sample size: n=5,000, the data is similar to the normal distribution.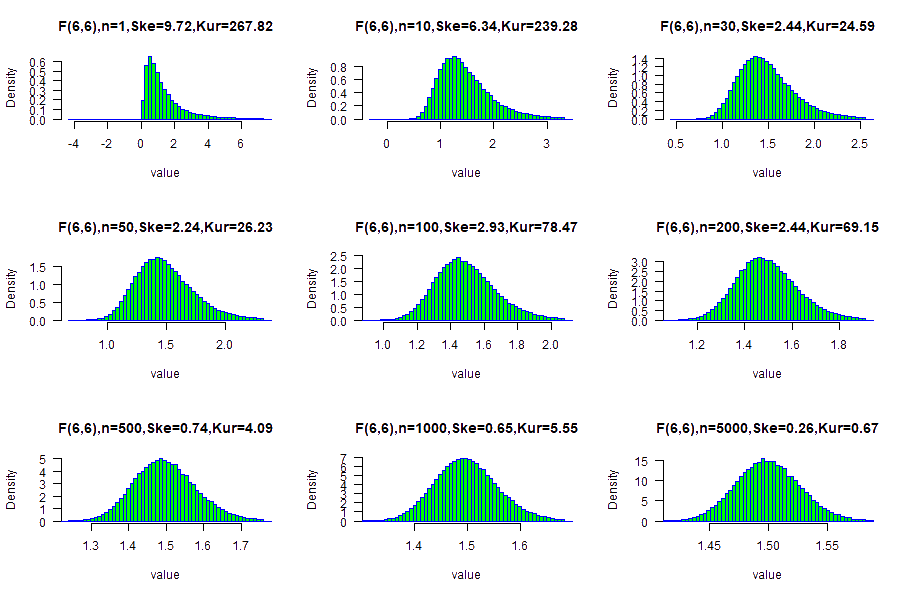

Very highly skewed data (10.2): F(7,7) distribution

Following a simulation results of F distribution with df₁=7 and df₂=7.
The calculated skewness( F(7,7) ) is 10.1559 .
The calculated excess kurtosis( F(7,7) ) is -166.714.
Only with large sample size: n=500, the data is similar to the normal distribution.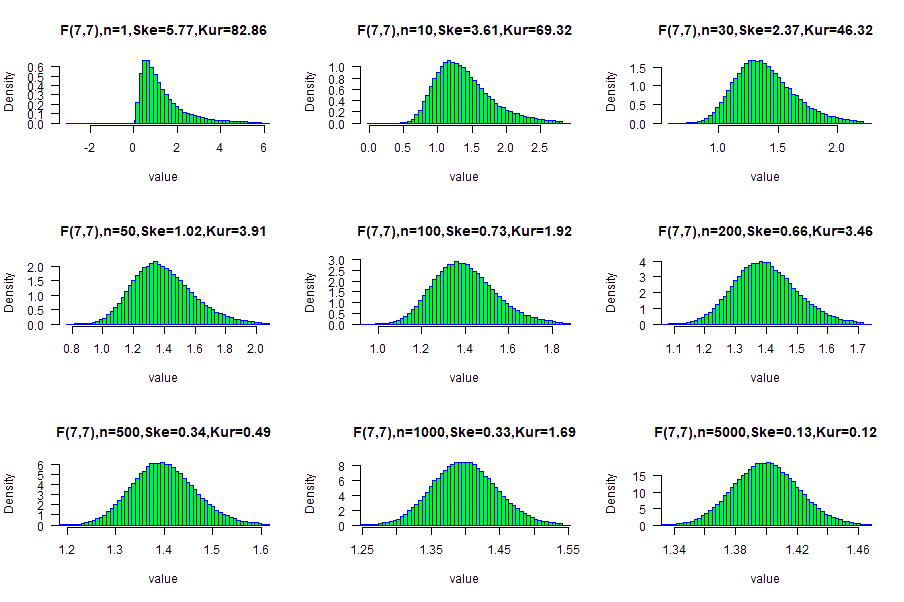

Highly skewed data (3.0): F(6,12) distribution

Following a simulation results of F distribution with df₁=6 and df₂=12.
The calculated skewness( F(6,12) ) is 2.9938 .
The calculated excess kurtosis( F(6,12) ) is 23.1667.
With small sample size: n=50, the data is similar to the normal distribution.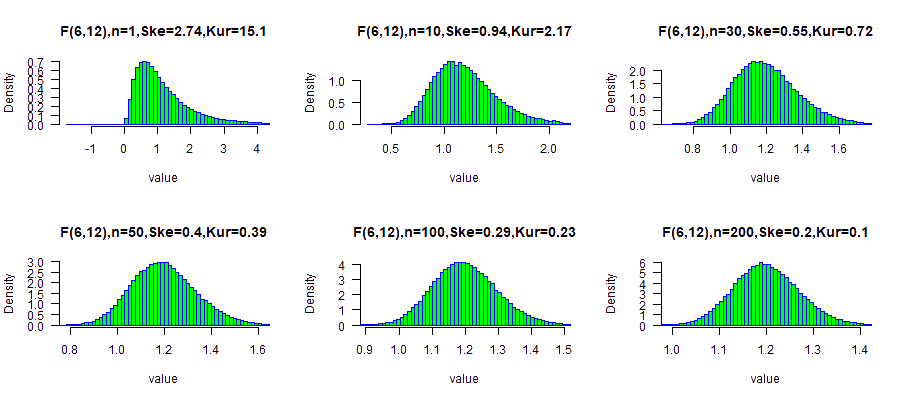

Moderate-Highly skewed data (1.0): F(30,47) distribution

Following a simulation results of F distribution with df₁=30 and df₂=47.
The calculated skewness( F(30,47) ) is 1.0444 .
The calculated excess kurtosis( F(30,47) ) is 1.8889.
With small sample size: n=10, the data is similar to the normal distribution.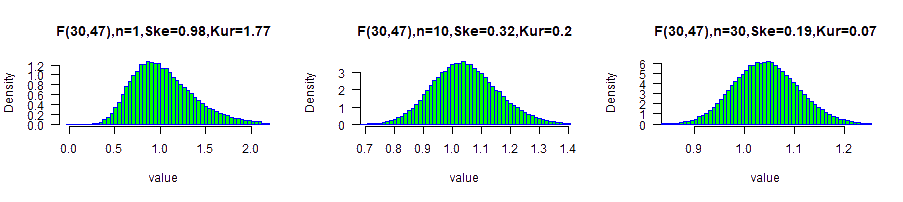

Symmetrical Uniform(0,1) distribution

The uniform distribution is symmetrical but flat. It doesn't look like the bell shape.

The calculated skewness( U(0,1) ) is 0.
$$The\ calculated\ Excess\ Kurtosis=-\frac{6}{5}=-1.2$$ With small sample size: n=10, the data is similar to the normal distribution.

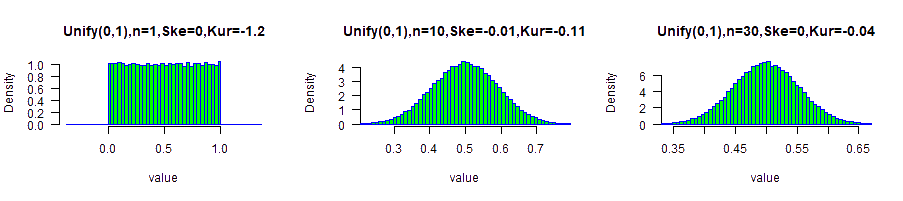
Failure examples

As you can see the CLT doesn't always work. In the following examples you may see that despite very large sample size, the distribution is still skewed.

Undefined skewed data: F(3,3) distribution

When DF₂≤4 the variance of the original distribution is not defined and when DF₂≤6 the skewness of the original distribution is not defined.
Following a simulation results of F distribution with df₁=3 and df₂=3.
The calculated skewness( F(3,3) ) is undefined .
The calculated excess kurtosis( F(3,3) ) is undefined.
You can see that even with a large sample size, n=100,000, the data is still extremely skewed.