One way ANOVA test (go to the calculator)

Video Levene's test Kruskal-Wallis test Tukey HSD test Bonferroni correction Sidak correction Holm method

The one way ANOVA test checks the null assumption that the mean (average) of two or more groups is equal. The test tries to determine if the difference between the sample averages reflects a real difference between the groups, or is due to the random noise inside each group.

When the ANOVA test rejects the null assumption it only tells that not all the mans equal. For more information, the tool also runs the Tukey HSD that compares each pair separately. The one way ANOVA model is identical to the linear regression model with one categorical variable - the group. When using the linear regression the results will be the same ANOVA table and the same p-value.

Assumptions

Independency - Independent groups, and independent observations that represent the population.
Normal distribution - The population distributes normally. This assumption is important for a small sample size. (n<30)
The ANOVA calculator runs the Shapiro Wilk test as part of the test run.
Equality of variances - the variances of all the groups are equal. The ANOVA test considered to be robust to the homogeneity of variances assumption when the groups' sizes are similar. (Maximum sample size/ minimum sample size< 1.5)
The ANOVA calculator runs the Levene's test as part of the test run.

Calculation

The model analyzes the differences between all the observations and the overall average and tries to determine if the differences are only random differences or also partially explained by the group. (similar to the linear regression).
As in the standard deviation calculation, we use the sum of squares instead of the absolute difference.

SST - the sum of squares of the total differences.
SSG/SSB - the sum of squares of the differences caused by the group. The calculation is similar to the SST but instead of using the entire difference between any observations and the overall average, it takes only the difference between the group's average and the overall average.
SSE/SSW - the sum of squares of the differences within the groups. The calculation is similar to the SST but takes only the differences between the observations and the groups' averages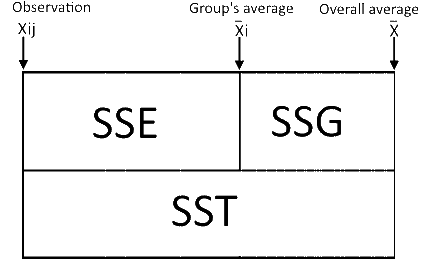

average

ANOVA table

Source	Degrees of Freedom	Sum of Squares	Mean Square	F statistic	p-value
Groups (between groups)	k - 1	$$SSG= \sum_{j=1}^{n_i}\sum_{i=1}^k (\bar{x}_{i}-\bar{x})^2 = \sum_{i=1}^k n_i(\bar{x}_i-\bar{x})^2$$	$$MSG = \frac{SSG}{k - 1}$$	$$F = \frac{MSG}{MSE}$$	P(x > F)
Error (within groups)	n - k	$$SSE=\sum_{j=1}^{n_i}\sum_{i=1}^k (x_{ij}-\bar{x_i})^2 = \sum_{i=1}^k (n_i-1)S_i^2$$	$$MSE = \frac{SSE}{n - k}$$
Total	n - 1	$$SST = \sum_{j=1}^{n_i}\sum_{i=1}^k (x_{ij}-\bar{x})^2 = SSG + SSE$$	$$Sample Variance = \frac{SST}{n - 1}$$

k - Number of groups.
n_i - Sample side of group i.
n - Overall sample side, includes all the groups (Σn_i, i=1 to k).
x_i - Average of group i.
x - Overall average (Σx_i,j / n, i=1 to k, j=1 to n_i).
S_i - Standard deviation of group i.

Effect Size

Priory effect size
If you are not sure what expected effect size value and type to choose, just choose "Medium" effect size and the tool will choose 'f' type and the relevant value. There are several methods to calculate the effect size.

Eta-squared
$$\eta^2=\frac{SSG}{SST} \qquad \eta^2=\frac{f^2}{1+f^2} \\ f^2=\frac{\eta^2}{1-eta^2}$$ This the ratio of the explained sum of squares random the total sum of squares. equivalent to the R² in the linear regression
Cohen's f-Method-1
The tool uses this method. $$f=\sqrt{\frac{SSG}{SSE}} $$ This the ratio of the explained sum of squares and the non-explained sum of squares (random noise).
Cohen's f-Method-2
$$f=\sqrt{ \frac{\sum_{i=1}^k(\bar{x}_{i}-\bar{x})^2}{k*\sigma^2}}\\ $$

When using equal group size both methods have the same result as n_i=n/k.
Method-1 $$f^2=\frac{ \sum_{i=1}^k n_i(\bar{x}_i-\bar{x})^2}{\sum_{j=1}^{n_i}\sum_{i=1}^k (x_{ij}-\bar{x})^2}$$ Method-2 $$\sigma^2=\frac{ \sum_{j=1}^{n_i}\sum_{i=1}^k (x_{ij}-\bar{x})^2}{n}\\ f^2 = \frac{ \sum_{i=1}^k(\bar{x}_{i}-\bar{x})^2*\frac{n}{k} }{\sum_{j=1}^{n_i}\sum_{i=1}^k (x_{ij}-\bar{x})^2}$$

Multiple comparisons

When running a single test the significance level (α) is the maximum type I error that allowed. If the p-value is bigger than the significance level the test accepts the null assumptions.
When running n multiple comparisons with significance level (α) in each comparison, the probability that at least one of the test will reject a correct null assumption is much bigger α'. $$\alpha'=1-(1-\alpha)^n$$ Example, when using 6 comparisons (n=6) and α=0.05 the allowed probability for type I error is:
α'=1 - (1 - 0.05)⁶ = 0.265
So if we want to keep α'= 0.05 we need to use much smaller significance level in each single test.
α - the allowed probability for type I error of a single test.
α' - the allowed probability for type I error of all the tests as a one package. For example, if we want α'=0.05 we should use α=0.00851.

Bonferroni correction

Bonferroni suggested α = α'/n
The correction assumes independent tests.

Bonferroni Correction Calculator

The number of tests / pairs.

Overall α':

Overall significance level.

Corrected α:

One pair's significance level.

Any change in any field will calculate the other fields. Change in n will calculate the corrected α, change in the overall α' will calculate the corrected α and change in the corrected α will calculate the overall α'.

Sidak Correction

The Bonferroni is not accurate, following the accurate calculation: $$\alpha'=1-(1-\alpha)^n \\ (1-\alpha)=\sqrt[n]{1-\alpha'}\\ \alpha=1-\sqrt[n]{1-\alpha'}$$

Sidak Correction Calculator

The number of tests / pairs.

Overall α':

Overall significance level.

Corrected α:

One pair's significance level.

When you use a corrected significance level of α = 0.025321 in any single test, the overall significance level α' = 0.05.
This is the probability to get type I error in at least one of the tests when all the null assumptions are correct in all the tests.

Holm Method

The Bonferroni/Sidak corrections are very consecutive, protecting against type 1 error at the expense of increasing type 2 error. The corrections assumes independent tests, this assumption is usually incorrect. If some of the tests have some dependencies the Bonferroni/Sidak corrections would be over protection.

The Holm correction supports better balance between the two errors. Following the steps

Rank test by the p-value results, R = 1 for the smallest p-value, R = n for the greater p-value.
$$\alpha_{(i)}=\frac{\alpha'}{n+1-R_{(i)}}$$
Stop on the first insignificance test, the next tests are insignificance. (H₀ accepted).

Holm Method Calculator

Overall α'

P-values

Corrected α

0.0125
0.0167
Stop
Stop

H₀

Rejected
Accepted
Accepted
Accepted

When entering data to P-values box, press comma , , Space or Enter after each value.
Change in the Overall α' or change in P-values will calculate the Corrected α and the H₀.
Just click anyway outside the input box, or press the calculate button.

Explanation of the original example numbers which includes three comparisons:
n = 4.
0.05 / (4 + 1 - 1) = 0.0167. Since 0.011 < 0.0125 this comparison is significant.
0.05 / (4 + 1 - 2) = 0.025. Since 0.026 > 0.0167 this comparison is not significant.
Since the second comparison is not significant we stop calculating the corrected α. Now all the rest comparisons are not significant. So only the first comparison is significant. (If we would continue calculating the next two corrected α the forth comparison would be significance, but this is not the algorithm).

Tukey HSD test / Tukey-Kramer test (go to the calculator)

The Tukey HSD (Honestly Significant different ) test is a multiple comparison test that compares the means of each combination. The test uses the Studentized range distribution instead of the regular t-test. It is only a two-tailed test, as the null assumption is equal means. The Tukey HSD test assumes equal groups and the Tukey-Kramer know to handle unequal groups, so the Tukey HSD test is a special case of the Tukey-Kramer test.
The ANOVA calculator executes both the ANOVA test, and the Tukey-Kramer test.

Assumptions

Independency - Independent groups, and independent observations that represent the population.
Normal distribution - The population distributes normally
Equality of variances - the variances of all the groups are equal.

Calculation

Calculating the following for each pair of groups: Group_i-Group_j
$$ Difference = |\bar{x}_i-\bar{x}_j|\\ SE=\sqrt{(\frac{MSW}{2}(\frac{1}{n_i}+\frac{1}{n_j})}$$ The test statistic $$ Q=\frac{Difference}{SE} $$ Calculating the p-value and the Q_1-α percentile, with the cumulative Studentized range distribution: $$p\text{-}value=P(X \leq Q,Groups, DFE)\\ P(X \leq Q_{1-\alpha})=1-\alpha $$ Confidence Interval $$CI = Difference \pm SE*Q_{1-\alpha}$$ Any difference that is larger than the critical mean is significant. $$Critical\;Mean=SE*Q_{1-\alpha}$$

Levene's test (go to the calculator)

The Levene's test checks the null assumption the standard deviation of two or more groups is equal. The test tries to determine if the difference between the variances reflects a real difference between the groups, or is due to the random noise inside each group.

The Levene's test run the ANOVA model of the absolute differences from each group's center, using mean or median as the group center.

Assumptions

Independency - Independent groups, and independent observations that represent the population.
Normal distribution - The population distributes normally. This assumption is important for a small sample size. (n<30)
The ANOVA calculator runs the Shapiro Wilk test as part of the test run.

Calculation

The general recommendation is to use mean for a symmetrical distribution, or sample size greater than 30, and median for asymmetrical distribution.
Since the median and the mean are almost the same in the symmetrical distribution, you may just use the median.
When using the median it is called the Brown-Forsythe test.

$$X'_{ij}=X_{ij}-\bar{X}_i.\\ \bar{X}_i \; is\;the\;mean\;of\;group\;i$$
$$X'_{ij}=X_{ij}-\tilde{X}_i.\\ \tilde{X}_i \; is\;the\;median\;of\;group\;i$$

Example

Levene's test example.
Observations $$\begin{bmatrix}Group1&Group2&Group3&\\1&3&13&\\2&4&15&\\2&\textbf{5}&16&\\ \textbf{3}& \textbf{6}&\textbf{16}&\\4&8&19&\\5&11&21&\\6&&22&\end{bmatrix}$$ Medians
$$\begin{bmatrix}Group1&Group2&Group3&\\3&5.5&16&\end{bmatrix}$$ Differences
In this example, we use differences from the medians.
$$\begin{bmatrix}Group1&Group2&Group3&\\2.0&2.5&3.0&\\1.0&1.5&1.0&\\1.0&0.5&0&\\0&0.5&0&\\1.0&2.5&3.0&\\2.0&5.5&5.0&\\3.0&&6.0&\end{bmatrix}$$ Now you can run a regular ANOVA test over the differences

Kruskal-Wallis test (go to the calculator)

The Kruskal-Wallis test is the equivalent non parametric test for the One way ANOVA test.
The KW test checks the null assumption that when selecting a value from each of n groups, each of these groups will have an equal probability of containing the highest value.
When the groups have a similar distribution shape, the null assumption is stronger and states that the medians of the groups are equal.
When using the KW test with two tests it is the same as the Mann-Whitney U Test.
When using the calculator you will get the same result as Mann Whitney U test calculator with Z approximation and no continuity correction.
The test tries to determine if the difference between the ranks reflects a real difference between the groups, or is due to the random noise inside each group.

When the ANOVA test rejects the null assumption it only tells that not all the mans equal. For more information, the tool also runs the Tukey HSD that compares each pair separately. The one way ANOVA model is identical to the linear regression model with one categorical variable - the group. When using the linear regression the results will be the same ANOVA table and the same p-value.

Assumptions

Independency - Independent groups, and independent observations that represent the population.
Variables - The group is a categorical variable, and the independent variable - the variable we compare, may be continuous or ordinal.
Similar shape and scale - This assumption is relevant only if the null hypothesis assumes equal medians.

Calculation

Test statistic

$$H=\frac{12}{n(n+1)}\sum_{j=1}^{k}\frac{R_j^2}{n_j}-3n(n+1)$$ R_j - the rank sum of group j. n_j - the sample size of group j..
n - the total sample size across all groups, n = n₁+...+ n_j. k - number of groups.

Calculation

$$X'_{ij}=X_{ij}-\bar{X}_i.\\ \bar{X}_i \; is\;the\;mean\;of\;group\;i$$
$$X'_{ij}=X_{ij}-\tilde{X}_i.\\ \tilde{X}_i \; is\;the\;median\;of\;group\;i$$