Test calculation

Right-tailed - for the goodness of fit test, the test of independence / the test for association, or the McNemar test, you can use only the right tail test.
The calculator includes results from the Fisher calculator, binomial test, McNemar Mid-p, simulation.
The continuity correction tends to overcorrect and increase the possibility of a type II error. Hence the resulting p-value is usually too large. It's controversial, so we recommend to leave it as false
Enter raw data directly
Enter raw data from excel

McNemar chi-square test

Matched pairs

Changes from group A to group B
Changes from group B to group A
Before \ AfterAB
Aa12
B23d

Enter sample data

Enter sample data

You may copy data from Excel, Google sheets or any tool that separate data with Tab and Line Feed.
Copy the data, one block of 3 consecutive columns includes the top header row and left header column, and paste below. example


It is okay to leave empty cells, empty cells or non numeric cells won't be counted

*Choose Expected Frequencies or Expected Probabilities.
The sum of the expected values must be equal to the sum of the observed frequencies or to one.
clock

Results

kNumber of categories
nSample size
χ²Chi square test statistic
DF
Phi effect (Φ)Φ=√(χ2/n)
validation message

Information

Hypotheses
H0: Model Fits
H1: Model Doesn't Fit
Test statistic
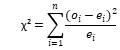
Chi2 statistic
χ² distribution
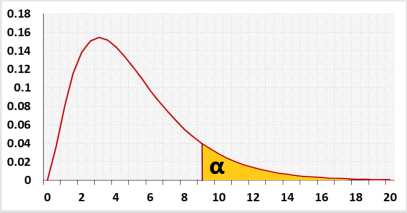
Chi-Squared distribution right tailed

Target: Check if the statistical model fits the observations.
The test uses Chi-square distribution.

McNemar chi-square test

The test checks only the cases when the status of the dichotomous variable was changed.
The null assumption is that the probability to switch from A to B equals the probability to switch from B to A, equals 0.5.

Before \ AfterAB
ANo changeA to B
BB to ANo change
The number of cases with no change, A to A or B to B, doesn't change the result of the McNemar test.

Chi-square test for independence

The null assumption is that the two categorical variables are independent.


R Code

The following R code should produce the same results:

Goodness of fit example: checking a fair dice.
Model: the probability of each side is equal - 1/6.
H0: fair dice.
H1: unfair dice.

The groups are the dice's numbers (1,2,3,4,5,6).
In this example, you throw the dice n times.
Expected frequencies - for each group are n/6.
Observed frequencies - the actual times each number appears.