Mann Whitney U test calculator (Wilcoxon rank-sum)

Non-parametric test
Video Informations Two Sample T-test
The test compares the probability to get higher value from group1 with the probability to get higher value from group2.

Test calculation

Enter raw data directly
Enter raw data from excel

Enter sample data

Header: You may change groups' name to the real names.
Data: When entering data, press Enter, , or Space after each value.

The tool ignores empty cells or non-numeric cells.

Enter sample data

You may copy data from Excel, Google sheets or any tool that separate data with Tab and Line Feed.
Copy the data, one block of 3 consecutive columns includes the header, and paste below.
Copy the data,
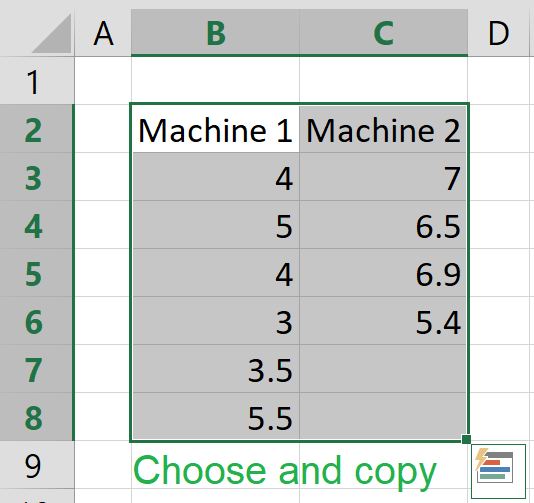
example from excel

It is okay to leave empty cells, empty cells or non numeric cells won't be counted

Results

Skewness Shape:


The difference between the expected SD and the sample SD

validation message

Information

Hypotheses
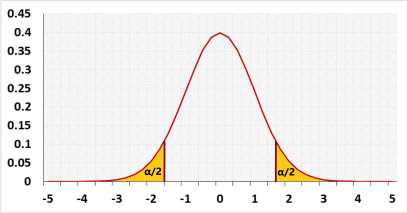
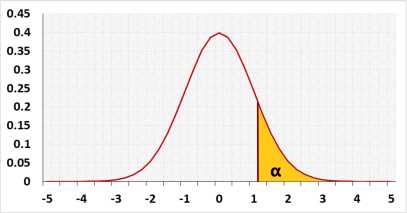
H0: Group1 ≥ = ≤ Group2
H1: Group1 < ≠ > Group2
Test statistic
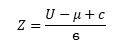
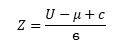
z statistic
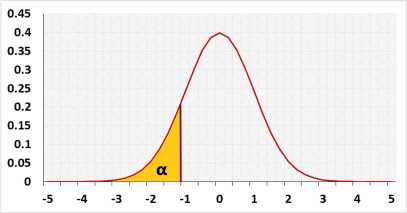
Normal distribution
z distribution left tailed z distribution two tailed z distribution right tailed
C - continuity correction, when U > μ: C = -0.5, when U < μ: C = 0.5

Target

Unlike t-test that compares the means, the Mann-Whitney U test compares a randomly selected value from group1 to a randomly selected value from group2.
When the two distributions have a similar shape you can use the test to compare also the medians.
When the two distributions have a similar symmetrical shape, you can use the test to compare also the means. more

Method

The mann whitney u test calculator may use three methods. We reccomend to use the "Automatic" method.
Automatic - when n1≤20 and n2≤20 and the data doesn't have ties, the tool uses the exact value, otherwise the tool uses the z approximation.
Exact - when n1≤20 and n2≤20 the tool uses the exact value, calculated base on all the possible combinations, otherwise the tool uses the z approximation.
Z approximation - the tool uses the z approximation.

Continuity correction - relevant only for the Z approximation. It is used since a continuous distribution is used to calculate a discrete distribution.

R Code

The following R code should produce similar results: